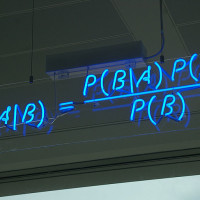
È il 2 di ottobre; le nubi coprono il cielo di Milano ma le temperatura sono nelle medie stagionali: tra i 10 e i 20 gradi. Nulla giustificherebbe l’acquisto di un girocollo di lana e di un piumino imbottito. Eppure… Non c’è vetrina di negozio di abbigliamento che non esponga i capi più pesanti e caldi di cui disponga. Folli? No bayesiani!
I vetrinisti non stanno facendo altro che applicare una delle teorie più discusse e affascinanti della statistica: l’inferenza bayesiana.
Nessun timore, dietro a due parole così sinistre si nasconde solo il seguente ragionamento: l’autunno e l’inverno sono succeduti all’estate per miliardi di anni. Ora l’estate sta finendo. Con un’elevata probabilità arriverà l’autunno.
Banale? Tutt’altro! A formalizzare per la prima volta il concetto fu il reverendo britannico Thomas Bayes (1702 – 1761) ma il teorema venne pubblicato postumo nel 1763; indipendentemente da lui anche Pierre Simone de Laplace arrivò alla sua enunciazione nel 1774.
Da un certo punto di vista il teorema di Bayes non è nient’altro che l’esplicitazione del metodo scientifico: a partire da una serie di dati già in nostro possesso possiamo formulare un’ipotesi; collezionando sempre nuovi dati possiamo continuamente aumentare (o rivedere) il grado di bontà delle nostre ipotesi.
Sostanzialmente il teorema di Bayes ci dice con quanta probabilità possiamo stimare che una determinata causa abbia generato un certo evento: una volta ottenuto un preciso risultato possiamo così valutare quanto questo si accordi con la teoria da cui siamo partiti; è una misura della bontà dell’ipotesi e della soggettività della ricerca che lo scienziato conduce.
Citando Giulio d’Agostini, professore associato a La Sapienza di Roma, e un esempio molto noto da lui ben descritto in “Reti Bayesiane: da modelli di conoscenza a strumenti inferenziali e decisionali” (S.Cenatempo, G.D’Agostini, A.Vannelli, 2010), qual è la probabilità che un cittadino scelto a caso all’interno della popolazione italiana sia affetto dal virus dell’HIV posto che sia risultato positivo al test? Considerando che il test dell’HIV può avere lo 0.2% di falsi positivi (ossia nello 0,2 % dei casi l’individuo non ha l’HIV anche se il test risulta positivo) ma non ha falsi negativi, calcoli alla mano (http://www.telecomitalia.com/content/dam/telecomitalia/it/archivio/documenti/Innovazione/NotiziarioTecnico/2010/fd_numero03/Bayesiane.pdf ) il teorema di Bayes ci dice che la probabilità di avere contratto l’HIV è del 45%: anche a test positivo è quindi più probabile non avere l’HIV. Calcoli simili si possono fare per i test diagnostici di tumori o sindrome di down http://www.zanichelli.it/fileadmin/catalogo/assets/a10.9788808062970.pdf .
Soprattutto in ambito medico la statistica Bayesiana risulta essere particolarmente utile e, al contempo , misconosciuta; ecco perché la Food and Drug Administration, l’ente governativo statunitense che si occupa della regolamentazione dei prodotti alimentari e farmaceutici adotta per i propri trial la statistica bayesiana e riporta sulle pagine del proprio sito un’intera sessione dedicata all’argomento (http://www.fda.gov/medicaldevices/deviceregulationandguidance/guidancedocuments/ucm071072.htm).
Ciò non significa che la statistica “frequentista” sia errata: un buon frequentista e un bayesiano arriveranno alla determinazione delle stessa probabilità; il teorema di Bayes offre uno strumento per non incappare in errori spesso nascosti e insidiosi nella distribuzione della probabilità: è un bastone a cui appoggiarsi per evitare gli ostacoli del senso comune.
Già perché il senso comune spesso ci induce all’errore…
Un caso tipico è quello del Monthy Hall, un gioco a premi americano ( Let’s make a deal) il cui conduttore Maurice Halprin, era noto con lo pseudonimo di Monty Hall.
Nel gioco il concorrente è posto davanti a tre porte chiuse ed è invitato a indovinare dietro quale delle tre porte si celi l’automobile in palio; dietro alle altre due porte si trovano due capre.
Supponiamo ora che il partecipante scelga la porta 1; prima di aprirla e scoprire cosa si celi dietro di essa il conduttore che sa dove sta l’automobile (questo è un punto fondamentale) apre la porta 3 dimostrando che dietro di essa si trova una capra. A questo punto il conduttore chiede al partecipante se vuole cambiare la porta. Noi cosa faremmo?
Il senso comune ci direbbe che la scelta è indifferente perché esiste il 50 % di possibilità che l’auto sia dietro la porta 1 o dietro la porta 2; un bayesiano al contrario cambierebbe subito la porta 1 con la porta 2 perché saprebbe in questo modo di raddoppiare la probabilità di vincita.
Ecco perché: quando il concorrente è davanti alle tre porte ha il 33,3% di possibilità di trovare l’auto dietro ogni porta. Sceglie la porta 1 con una possibilità di vittoria del 33,3%; questo significa che nel 66,6% dei casi l’auto sarà dietro la porta 2 o 3; aprendo la porta 3 e scoprendo dietro di essa una capra, il 66,6% di trovare l’auto ricadrà interamente sulla porta 2.
Il punto fondamentale che porta ad una distribuzione diversa da quella suggerita dal senso comune sta nel fatto che il conduttore non è libero di aprire una porta a caso ma deve necessariamente aprire una porta dietro la quale vi sia una capra; è la conoscenza del dato che cambia la distribuzione statistica; provare per credere! http://it.wikipedia.org/wiki/Problema_di_Monty_Hall
Verrebbe da chiedersi perché un teorema così utile sia stato quasi dimenticato per secoli; la motivazione è che il calcolo necessario per svilupparlo correttamente nei casi complessi è tutt’affatto banale.
Solo con i moderni calcolatori possiamo essere in grado di applicare l’inferenza Bayesiana ad una serie di variabili (o nodi) ricostruendo quelle che vengono chiamate reti bayesiane in grado di monitorare sistemi complessi; le reti bayesiane e i software implementati per la loro costituzione sono utili oggi per l’individuazione della malattia da cui è affetto un individuo (posto che più malattie possano dare gli stessi sintomi) facendo incrociare sintomi e stili di vita; vengono usate nei filtri anti-spam oppure nei musei per realizzare narrazioni audiovisive in funzione del percorso intrapreso e del tempo speso da un visitatore nelle diverse sale di museo. http://alumni.media.mit.edu/~flavia/Papers/flavia_mw2002.pdf
Oggi il “controverso teorema” sta vivendo un momento di grande successo, comparendo sia in articoli di riviste scientifiche (circa un quarto degli articoli scientifici usa la statistica bayesiana, Bayes’ Theorem in the 21st Century, Bradley Efron, Science 7 June 2013: Vol. 340 no. 6137 pp. 1177-1178) sia in review e commenti di varia natura (dalla giurisprudenza – “Science and law: Improve statistics in court – Norman Fenton, Nature, 479, 36–37, 03 November 2011 – all’economia, passando per le telecomunicazioni) che spingono sempre più all’utilizzo dell’inferenza bayesiana in ogni campo del sapere. Ma non è sempre stato così: il piccolo gruppo di statistici bayesiani attivi in America, in pieno maccartismo, veniva considerato “un-American” e definito dai colleghi dell’Harvard Business Scholl “socialist and so-called scientist” (Statistics: Known unknowns Andrew Robinson Nature475,450–451 (28 July 2011).
E se ora scriverete “bayesian statistic” su google per averne un quadro più completo vi renderete conto di quante applicazioni possa avere un solo teorema, senza dimenticare che google stesso farà la sua ricerca usando, ovviamente, algoritmi bayesiani.





