La statistica è una materia che generalmente non resta troppo simpatica. “Già, perché se mangi due polli e io nessuno, per gli statistici ne mangiamo uno a testa” è la tipica argomentazione da bar in merito.
“Ma oltre alla media c’è anche la deviazione standard” potrebbe essere una replica. Che non avrebbe colto, però, il succo del discorso: la statistica tradizionale è sembrata un po’ limitata nel suo guardare il mondo reale, del resto, anche ad alcuni studiosi come l’ingegnere e ricercatore iraniano (naturalizzato statunitense) Lotfi Asker Zadeh.
Secondo quest’ultimo la parziale cecità della statistica deriverebbe dal principio aristotelico del tertium non datur: un elemento appartiene o non appartiene ad un insieme; un evento si verifica o non si verifica e così via. Ma le cose, nel quotidiano, non vanno proprio in questo modo. Com’è più corretto classificare il pollo, ad esempio: come uccello che vola o no?
E allora, come gestire, se non in parte forzandoli, i dati sperimentali? Con un nuovo modo di ragionare: il pensiero fuzzy introdotto per l’appunto da Zadeh nell’articolo Fuzzy Sets[i] del 1965.
Il termine fuzzy può essere tradotto con “sfocato”, “sfumato” o aggettivi simili; l’idea di base è che, considerando l’appartenenza di un elemento a un insieme come un concetto anche parzialmente indeterminato, si possa riuscire a descrivere i fenomeni affetti da incertezza in modo migliore.
In logica ciò ha implicato il passaggio a un livello di verità continuo – o, al limite, di più valori discreti – in sostituzione dei classici (e soli) valori di falso e vero.
|
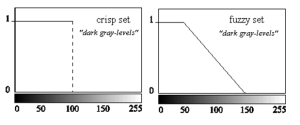
Figura 1: Classificazione di un’immagine scura a partire dal livello di grigio[ii]. Due sole classi (approccio standard) o infinite? |
Ciò ha richiesto una ridefinizione di molti strumenti come l’implementazione degli operatori elementari AND, OR, NOT.
Ad oggi il fuzzy pensiero è stato impiegato con successo in varie discipline: informatica, teoria dei sistemi, ingegneria, economia e via dicendo. Con la statistica il matrimonio è avvenuto con la teoria delle possibilità, come ha suggerito ancora Zadeh in un celebre articolo[iv] del 1978.
Il primo aspetto da evidenziare nella nascente teoria, detta anche “delle probabilità imprecise”, è il drastico cambio di prospettiva: probabilità (che evento si verifichi nel futuro) contro plausibilità (che un evento già avvenuto si sia verificato).
Un altro elemento è l’uso di due misure per l’evento (o proposizione) p, anziché una, la consueta probabilità Prob(p). La prima, detta possibilità, per misurare il grado di ragionevolezza di una proposizione p. La seconda, chiamata necessità e definita in termini del complementare di p (“¬p”), per indicare quanto p “avrebbe dovuto esser vera”.
Ultimo e forse più dirompente aspetto è l’indipendenza reciproca di possibilità e necessità. Ciò consente anche di disegnare un piano per classificare il tipo di conoscenza posseduto.
|
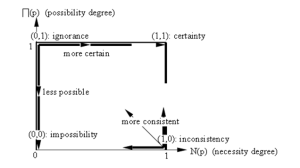
Figura 2: Il piano possibilità, necessità.[v] |
Un concetto obiettivamente non immediato da digerire e che, infatti, provocò svariate critiche dai seguaci del classico assioma di normalizzazione Prob(p)=1-Prob(¬p), che trasferito in ambito di possibilità implicherebbe una sua perfetta coincidenza con la necessità.
Eppure, a ben riflettere, anche noi non pensiamo sempre che più probabilità vuol dire maggiore obbligo; lo facciamo solo se abbastanza sicuri di aver ben compreso il fenomeno. Osservando, ad esempio, la nostra lavatrice funzionare è plausibile dire (possibilità alta) che, con la botta a caso che gli abbiamo dato, questa sia ripartita nel modo giusto. Eppure questo non avrebbe dovuto succedere (necessità bassa) dato che le lavatrici notoriamente non si aggiustano così. E allora? E’ successo, semplicemente, che l’abbiamo messa a posto senza sapere come, ossia che siamo vicini al punto di ignoranza di Figura 3.
L’algebra delle possibilità è caratterizzata anche da altri passaggi a prima vista sorprendenti. Ad esempio la possibilità delle proposizioni composte unione (x+y) e intersezione (xy) non è gestita tramite addizione e moltiplicazione – come in teoria delle probabilità – ma con operatori di massimo e minimo.
MA TUTTO QUESTO COSA C’ENTRA CON IL PENSIERO FUZZY?
Zadeh, oltre a dimostrare formalmente che una variabile fuzzy induce una distribuzione di possibilità, espresse il concetto così: una variabile “sfumata” sta alla teoria delle possibilità come una variabile aleatoria sta a quella delle probabilità.
E’ difficile condensare il ragionamento di dettaglio in poche righe e qui non sarà riportato. A supportare il parziale atto di fede che stiamo chiedendo, possiamo portare, però, alcune evidenze. Intanto: una funzione di appartenenza fuzzy – quella per cui, ad esempio, possiamo dire che il nostro pollo appartiene a un livello 0.2 all’insieme dei volatili – ha le stesse caratteristiche di continuità e variabilità in [0,1] di una funzione di possibilità o necessità. Inoltre: possibilità e necessità si combinano esattamente come lo farebbero due proposizioni in logica fuzzy.
E le applicazioni, potremmo chiederci?
In ricerca applicata[vi] è possibile trovare varie soluzioni basate sulla teoria della possibilità[vii]. Gli ambiti principali sono: l’analisi di data sets affetti da particolari incertezze[viii], la diagnosi (di guasto per applicazioni aerospaziali o di tipo medico), la robotica e l’intelligenza artificiale (per supportare il movimento autonomo in spazi occupati da oggetti). Si trovano, però, anche casi in teoria dell’argomentazione e in psicologia cognitiva.
Poco numerosi sono, d’altra parte, i manuali tecnici di prodotti che fanno analoghe citazioni. Potrebbe essere, però un semplice problema lessicale. Se, infatti, cambiamo l’elenco delle nostre parole chiave da “teoria delle possibilità” a “logica fuzzy” il numero dei casi esplode. Esempi in cui magari non sarà presente l’uso di distribuzioni di possibilità e necessità – ma ad esempio dei classici concetti di probabilità, media, varianza etc… – ma in cui i dati saranno necessariamente elaborati con l’uso di logiche multilivello o funzioni di attivazione continue (come quella di Figura 1) e che saranno quindi applicazioni quantomeno parziali della statistica fuzzy.
In questa casistica rientra tutto il settore del trattamento delle immagini[ix] con le tecniche di evidenziazione dei contrasti, miglioramento, segmentazione e rilevazione dei bordi. Loro usi documentati riguardano, oltre che la fotografia digitale, il riconoscimento ottico dei caratteri[x] (quello implementato da vari scanner da ufficio nonché nei sistemi di rilevamento automatico delle infrazioni per corsie preferenziali e ZTL) e la filmografia (famoso è rimasto il motore grafico MASSIVE, usato per il film “Il Signore degli Anelli”).
C’è, poi, tutto l’ambito delle applicazioni industriali dell’intelligenza artificiale debole: da quelle utilizzate nei video games (anche molto famosi come Unreal o Civilization[xi]), alle reti neurali per la ricerca di giacimenti di metalli[xii], ai sistemi esperti per vari tipi di utilizzi.
C’è, infine, tutto il settore dell’automazione: dall’esempio storico della metropolitana di Sendai in Giappone[xiii], a quello più recente della Monorotaia di Tokyo[xiv]. Ciò senza contare il riferimento a microcontrollori[xv] a PLC per uso industriale[xvi] o a dispositivi ancora più comuni. Come, ad esempio, alcuni condizionatori per aria[xvii] migliori perché in grado di ragionare sul livello di confort avvertito dal loro proprietario (variabile fuzzy) e non semplicemente sul valore di temperatura (variabile aleatoria). O certi tipi di lavatrici che stabiliscono da sole, in base al peso della biancheria o alla torbidezza dell’acqua, le condizioni ottimali di lavaggio.
In conclusione possiamo dire che, rendendo statistica e logica più vicine al modo con cui l’uomo percepisce il mondo, è stato possibile ottenere nuove risposte, elaborare meglio i dati e rendere vari artefatti più confortevoli e intelligenti.
Certo, tutto questo ha avuto un prezzo: “concettualmente, matematicamente e computazionalmente [tutto è diventato] più complesso”, usando ancora una volta le parole del professor Zadeh.
Per cui una cosa non dovremo aspettarci dalla teoria delle possibilità o dalla logica fuzzy: che riusciranno a rendere la statistica più simpatica nelle chiacchere da bar.
[i] L. A. Zadeh, “Fuzzy Sets”, Information and Control, 1965. URL: http://www-bisc.cs.berkeley.edu/Zadeh-1965.pdf
[ii] University Of Waterloo, Fuzzy Image Processing, URL: http://tizhoosh.uwaterloo.ca/Fuzzy_Image_Processing/set.htm
[iii] Calvin College, Getting Started with Fuzzy Logic, URL: https://www.calvin.edu/~pribeiro/othrlnks/Fuzzy/fuzzyops.htm
[iv] L. A. Zadeh, Fuzzy Sets As A Basis For A Theory Of Possibility, North-Holland Publishing, 1978. URL: http://www.cs.berkeley.edu/~zadeh/papers/Fuzzy%20sets%20as%20a%20basis%20for%20a%20theory%20of%20possibility-1978.pdf
[v] L. A. Zadeh, Probability Theory and Fuzzy Logic, December 9, 2002 URL: http://www.ieeesmc.org/announcements/Newsletter/JAN2003/Probability%20Theory%20and%20Fuzzy%20Logic.pdf
[vi] K. S. Animesh, B. V. Bandamwar, “Fuzzy Logic Based Systems In Management And Business Applications”, International Journal of Innovative Research in Engineering & Science, 2013, http://www.vnmpublication.com/IJIRES/January%202013/1.pdf
[vii] Scholarpedia, Possibility Theory, http://www.scholarpedia.org/article/Possibility_theory
[viii] Departamento de Lenguajes y Ciencias de la Computación, FSQL, A Fuzzy SQL, http://www.lcc.uma.es/~ppgg/FSQL/
[ix] University Of Waterloo, Examples, URL: http://tizhoosh.uwaterloo.ca/Fuzzy_Image_Processing/examples.htm
[x] Freescale Semiconductor Inc, Optical Character Recognition Using Fuzzy Logic, URL: http://www.freescale.com/files/microcontrollers/doc/app_note/AN1220_D.pdf
[xi] M. Pirovano, The use of Fuzzy Logic for Artificial Intelligence in Games, 2012, Università di Milano, URL: http://homes.di.unimi.it/~pirovano/pdf/fuzzy_ai_in_games.pdf
[xii] P. Tahmasebi, A. Hezarkhan, “Application of Adaptive Neuro-Fuzzy Inference System for Grade Estimation; Case Study, Sarcheshmeh Porphyry Copper Deposit, Kerman, Iran”, Australian Journal of Basic and Applied Sciences, 2010, URL:http://www.ajbasweb.com/ajbas/2010/408-420.pdf
[xiii] B. Kosko, S. Isaka, “Fuzzy Logic”, Scientific American, 1993, URL: http://sipi.usc.edu/~kosko/Scientific%20American.pdf
[xiv] Lehigh University, Computer Science & Engineering, Fuzzy Logic, URL: http://www.cse.lehigh.edu/~munoz/CSE335/classes/fuzzy_logic.ppt
[xv] Freescale Semiconductor Inc, CPU12RM User Manual, URL: http://www.freescale.com/files/microcontrollers/doc/ref_manual/CPU12RM.pdf
[xvi] Fuzzytech, Recent Successful Fuzzy Logic Applications in Industrial Automation, URL: http://www.fuzzytech.com/e/e_a_plc.html
[xvii] Fuzzytech, Fuzzy Logic and NeuroFuzzy in Appliances, URL: http://www.fuzzytech.com/e/e_a_esa.html